北师大版小学数学四年级上册
第一单元知识要点
一、数一数：
通过数一数、拨一拨认识“十万”。一个一个的数，十个一是十。一十一十的数，十个十是一百。一百一百的数，十个一百是一千。一千一千的数，十个一千是一万。一万一万的数，十个一万是十万。
二、认识更大的数：
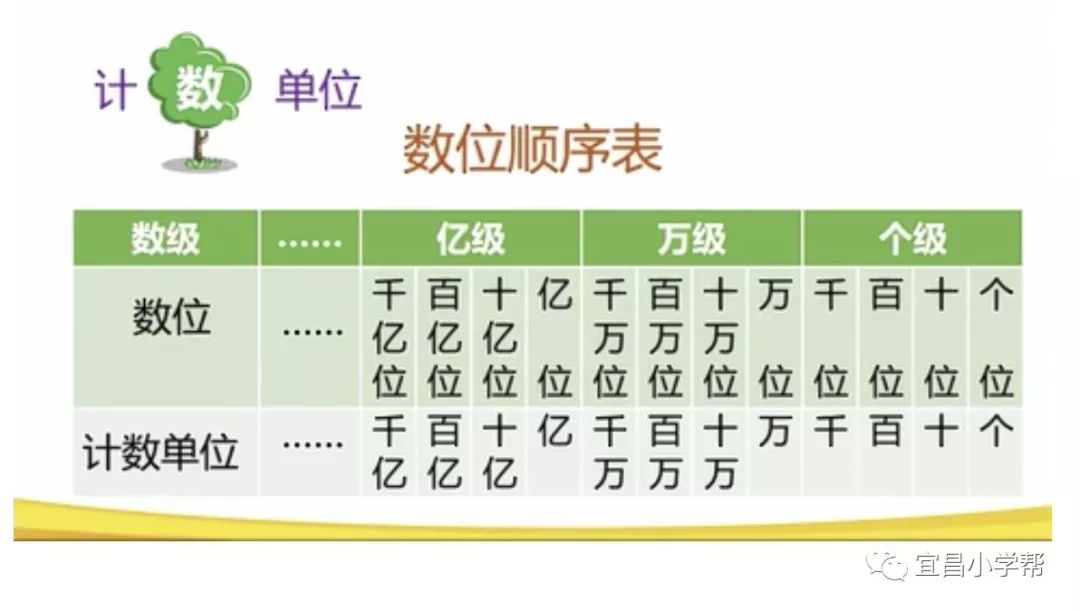
1认识数级、数位、计数单位，并了解它们之间的对应关系。从个位起四位一级，个位、十位、百位、千位是个级，万位、十万位、百万位、千万位是万级，亿、十亿位、百亿位、千亿位是亿级。
2、十进制计数法。相邻两个计数单位之间的进率是十，也就是十进制关系。
3、数数。能一万一万地数，十万十万地数，一百万一百万地数……                   

三、人口普查
这节主要学习的是亿以内数的读法、写法。
1、亿以内数的读数方法。
  含有个级、万级和亿级的数，必须先读亿级，再读万级，最后读个级（即从高位读起）。读亿级或万级的数按照个级的读法读，然后在后面加上亿“字”或万“字”。，每级中间连续有几个零，都只读一个零。每级末尾不管的零不读。
2、亿以内数的写数方法。
从高位起，按照数位的顺序写，中间或末尾哪一位上一个数字也没有，就在那一位上写0。
四、国土面积
1、比较数大小的方法。
多位数比较大小，如果位数不同，那么位数多的这个数就大，位数少的这个数就小。如果位数相同，从左起第一位开始比起，哪个数字大，哪个数就大。如果左起第一位上的数相同，就开始比第二位……直到比出大小为止。
2. 多位数的改写。
改写的意义。为了读数、写数方便。
改写以“万”或“亿”为单位的数的方法。
（1）把整万的数改写成以“万”为单位的数，就是把原数末尾的4个0去掉，在余下的数末尾写上“万”字；
(2)把整亿的数改写成以“亿”为单位的数，把原数末尾的8个0去掉，在余下的数末尾写上“亿”字。
五、求近似数
1.近似数是四舍五入省略“亿”或“万”尾数，写以“万”或“亿”为单位。
2、用四舍五入法保留近似数的方法。
取近似数的时候，如果尾数的最高位数字是4或者比4小，就把尾数舍去，改写成0；如果尾数的最高位是5或者比5大，就把尾数改写成0后，还要向前一位进一。
六、从结绳计数说起。
本节主要是认识自然数。
表示物体个数的0,1,2,3,4,5,6,7,8,9,10,11,12，…都是自然数。一个物体也没有，用0表示。0也是自然数。
北师大版小学数学四年级上册
第二单元知识要点
一、线的认识
1、线段
（1）两个端点
（2）有一定的长度，不能向两端延伸。

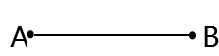
读作：线段AB（或BA）
2、直线
（1）没有端点
（2）可以向两个方向无限延伸。

读作：直线AB（或BA）
3、射线
（1）只有一个端点
（2）只能向一个方向无限延伸

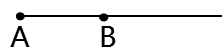
读作：射线AB
4、比较三种线的特征
类型
图形
端点数
延伸
长度
线段
2个
不能延伸
有限长
射线
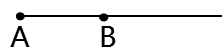
1个
向一个方向无限延伸
无限长
直线
无端点
向两个方向无限延伸
无限长
5、距离：下图中线段AB的长度就是A，B两点之间的距离。
两点之间所有连线中线段最短

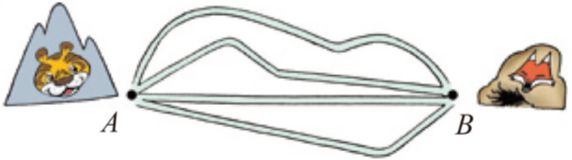
二、 相交与垂直
1、相交教材上包括两条已经相交和延长后一定相交两种情况。本节课主要研究的是相交的一种特殊形式，当两条直线相交成直角时，我们就说这两条直线互相垂直。如右图。我们就说其中一条直线是另一条直线的垂线，相交的一点叫垂足。

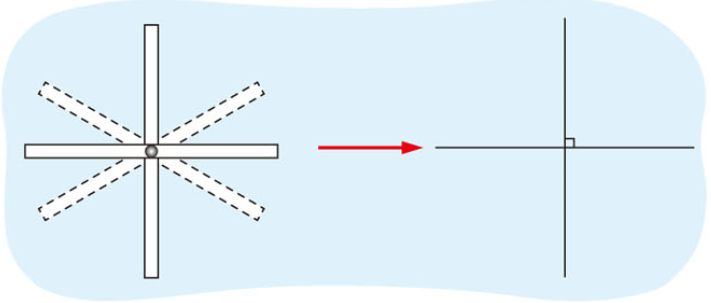
2、垂线可以用纸折叠方法得到。也可以借助三角板上的直角画垂线。

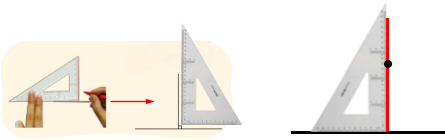
3、从直线外一点到这条直线的所有连线中，垂线最短。我们说这条线段是这点到这条直线的距离。

三、平移与平行
1平行线的定义：在同一平面内，不相交的两条直线叫平行线。这个定义要理解两点：一是两条直线必须在同一平面内，二是不相交。
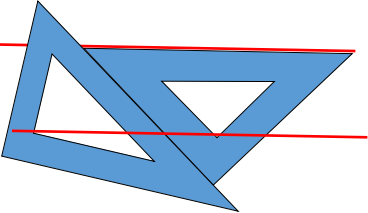
2平行线的画法。用纸折叠的方法得到平行线。在方格纸上画平行线。我们也可以借助直尺和三角板画平行线。

四、旋转与角
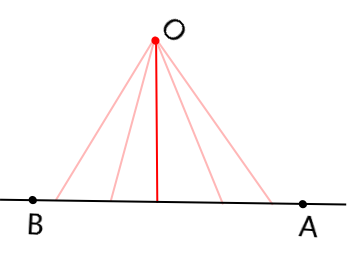
1如右图所示：用纸条折成一个活动角，固定一条边，旋转另一条边就可以得到角。

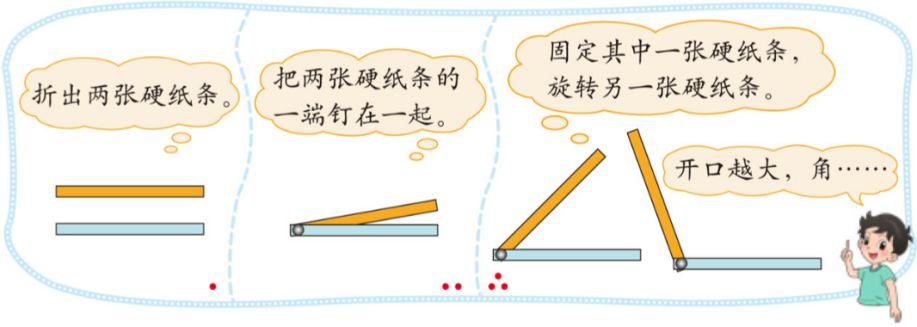
2、角的的定义：从一点引出的两条射线组成的图形叫做角。角的大小与两边叉开的程度有关，两边开口越大角就越大。角的大小与两边的长短无关。
3、角的分类：

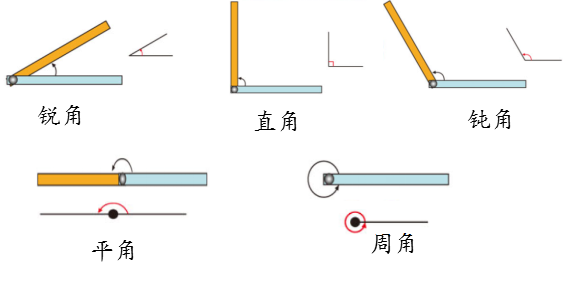
4、直角的度数是90°。平角的两边在一条直线上，平角的度数是180°。周角的两条边重合在一起，周角等于360°。
 1周角=2平角=4直角
五、角的度量（一）（二）
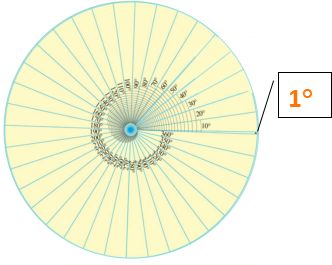
1、认识1°， 将圆平均分成360份，其中的1份所对的角的大小叫做1度（记作1°），通常1°作为度量角的单位。1周角=360°，1平角=180°，1直角=90°。
2、认识量角器。
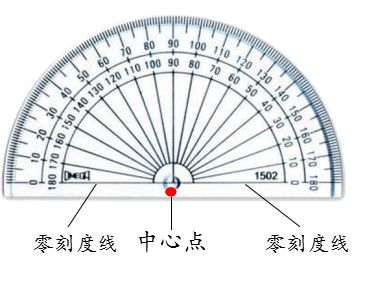
量角器把半圆平均分成180份。如右图：它有内外两圈刻度线，内圈刻度是按逆时针从0°到180°，外圈刻度是按顺时针从0°到180°。一个
中心点。两条0°刻度线。

3、用量角器量角的方法。
先将角的顶点和量角器的中心点重合，再把零刻度线与角的一条边重合，然后看角的另一边落在那个刻度纸上，此时这个角的度数就是多少。注意：量角器分为外圈和内圈，当零刻度线在内圈时，要读取内圈的度数，外圈时，读取外圈的度数。

4、用量角器画角的方法。
（1）先画一条射线。
（2）把量角器的中心和射线的端点重合,零度刻度线和射线重合。
（3）在量角器你要画的角的度数的刻度的地方记一个点。
（4）从射线的端点出发,通过新记的点,再画一条射线。这两条射线所夹的角就是你所要画的角。
北师大版小学数学四年级上册
第三单元知识要点
一、卫星运行时间（三位数乘两位数）
1、估算三位数乘两位数的乘积范围：用四舍五入法进行估算。
（1）可以把两个乘数（因数）都看作接近的整十、整百数，然后再将近似数相乘。A两个乘数都估小；b两个乘数都估大；c一个乘数估小，另一个乘数估大。  
（2）把其中的一个因数看作接近的整十、整百数 ，另一个因数不变，然后相乘。
2、准确计算三位数乘两位数的积。
 （1）把第二个乘数拆成几十和几个一，分别去乘第一个乘数，最后把两次的乘积加起来。

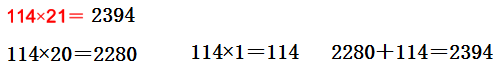
（2） 把第二个乘数分成两数相乘的形式，再和第一个乘数乘。

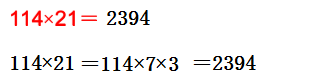
（3）列表计算求积。

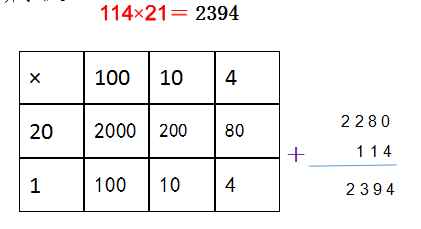
（4）竖式计算。

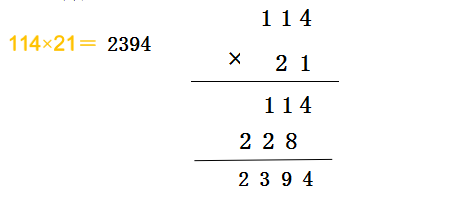
（5）三位数乘两位数的计算方法：先用两位数个位上的数去乘三位数，所得的积的末尾要和个位对齐，然后再用两位数十位上的数去乘三位数，所得的积的末尾要和十位对齐，哪一位满几十就向前一位进几，最后把两次乘得的积加起来。
（6）中间和末尾有0的乘数的计算方法。
二、有多少名观众
1、实际生活中的估算，估算的方法及注意事项：要将因数估成整十、整百或整千的数。估算时注意，要符合实际，接近精确值。
2、掌握乘法的估算方法，在解决具体问题的过程中，能应用合适的方法进行估算。能与同学交流自己估计的方法，培养良好的学习品格，形成积极、主动的估算意识。
三、神奇的计算工具

1、在学生原有基础上进一步认识并会使用计算器。


2、利用“M+”存储键，“MR”提取键，计算四则运算的题目。
3、用计算器计算的程序：

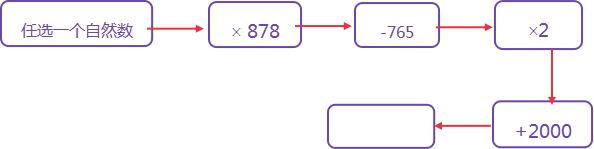
4、了解计算机中使用的是二进制计数法，就是满2进1。
四、有趣的算式
1、第一关：奇妙的宝塔。
规律：从积与乘数中1的个数发现每一个乘数中数字1的个数有几个，积的排列次序就从1排到几，再倒回到1，所以每个积就像一座宝塔似的。
1×1=1
11×11=121   
111×111=12321
1111×1111=1234321
11111×11111=123454321
111111×111111=12345654321
1111111×1111111=1234567654321
2、第二关：神奇的9
99×99=9801 
999×999= 998001
9999×9999=99980001
规律：它们的积都以数字98开头，以1结尾，中间填0，0的个数是算式中一个乘数里9的个数减1得来的。
3、第三关：奇怪的１４２８５７。
142857×1=142857     142857×3=428571
142857×2=285714     142857×4=571428
规律：用142857的个位上的7乘第二个乘数，确定积的个位是几，然后在142857中找到这个数，把它及前面的数一起移到积的后面，剩余的一部分移到积的开头，如果剩余两部分，把后面的部分放前面。如142857×2，7×2＝14，积的个位就是4，先从142857中找到4，把4及前面的1写在得数的后面，其余的2857就写在开头，所以142857×2＝285714。
4、第四关：寻找神秘的数。
在0-9十个数字中，随意选出4个你喜欢数字。
规则：将四个数字组成数字不重复的最大四位数和最小的四位数。如：1，2，5，0。最大四位数：5210，最小四位数：1025，然后两数相减，并把得出的四位数字重新组成一个最大的四位数与最小的数，再次相减……在不断重复的过程中，得到的最后结果如果是6174，就是好孩子，否则就不是好孩子。
北师大版小学数学四年级上册
第四单元知识要点
一、买文具
1、只有加减或只有乘除运算时，从左到右依次计算。既有加减又有乘除运算时，先算乘除后算加减。如果有括号，要先算（）里的，再算[ ]里的，最后算括号外面的。
2、用“小括号”“中括号”改变原式的运算顺序。
二、加法交换律和乘法交换律
 1、加法交换律：两个数相加，交换加数的位置，和不变。用字母表示为：a+b=b+a 。
2、乘法交换律：两个数相乘，交换乘数的位置，积不变。用字母表示为：a×b=b×a
三、加法结合律
1、加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。用字母表示为：(a+b)+c=a+(b+c) 。
2、应用加法运算律进行简便计算 在连加计算中，当某些加数相加可以凑成整十、整百、整千的数时，运用加法运算律可使计算简便。
3、口诀：连加计算仔细看，考虑加数是关键。整十、整百与整千，结合起来更简单。运算定律记心间，交换位置和不变。结合定律应用广，加数凑整更简便。
4、减法的运算性质：
（1）一个数连续减去两个数等于这个数减去这两个减数的和。用字母表示：a-b-c=a-(b+c)
（2）一个数减去两个数的和等于这个数连续减去和里每个加数。 
四、乘法结合律
1、乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘；或者先把后两个数相乘，再和第一个数相乘，积不变。用字母表示为：(a×b)×c=a×(b×c)
2、应用乘法运算律进行简便计算 在连乘计算中，当某两个乘数的积正好是整十、整百、整千的数时，运用乘法运算律可使计算简便。
3、运用分解的方法，将某个乘数拆分成几个数相乘的形式，使其中的乘数与其他乘数的乘积“凑整”。如;25X32=25X(8X4)=25X4X8
=100X8=800
4、除法的运算性质：
（1）一个数连续除以两个数（每次都能除尽）等于这个数除以这两个除数的积。
（2）一个数除以两个数的积等于这个数连续除以积里每个乘数。 
五、乘法分配律 
1、乘法分配律：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，结果不变。这叫做 乘 法 的 分 配 律。用字母表示：a×（b+c）= a×b + a×c
2、乘法分配律的应用
（1）乘法分配律正应用：直接利用a×（b+c）= a×b + a×c进行简便计算。如：8×(40+5)
（2）乘法分配律逆应用：利用a×b + a×c=a×（b+c）进行简便计算。如：8×47+8×53
（3）乘法分配律的特殊应用。
如：63×99+63 =63X（99+1）=63X100=6300     
88X25=（80+8）X25
=80X25+8X25=2000+200=2200